Clustering
In vielen Anwendungsgebieten wird versucht grosse Datenmengen automatisch aufzuteilen und nach gemeinsamen Eigenschaften zu gruppieren.
Clustering bedeutet die automatische Gruppierung einer Menge von Objekten zu vorher unbestimmten Gruppen, so daß die Beziehungen zwischen Objekten innrehalb einer Gruppe enger sind als zwischen Objekten verschiedener Gruppen.
Diese Objekte können sein:
- Texte
- einzelne Wörter
- Wortgruppen
- Bilder und andere graphische Objekte
- Audiosequenzen
- Strukturformeln
- ...
Gerade bei der immer stärker zunehmenden Menge an elektronisch verfügbaren Dokumenten sind automatische Verfahren zum Aufdecken der Abhängigkeiten notwendig. Zur Gruppierung von Ähnlichen Dokumenten in Kategorien, wo jede Kategorie ähnliche Merkmale besitz und sich von anderen Kategorien stark unterscheidet, stehen Clusteringverfahren zu Verfügung.
Dieses Vorgehen ähnelt einer automatischen Klassifizierung von Dokumenten. Der Unterschied zwischen Klassifizierung und Clustering ist, daß bei der Klassifizierung die Kategorien und ihre typischen Eigenschaften schon vor der Berechnung bekannt sind. Klassifikation ist die Gruppierung der Objekten anhand von Regeln, die entweder vorgegeben oder von selbstlernenden Systemen aus einer Menge von Beispieldokumenten erzeugt werden.
Beim Clustering hingegen ergeben sich die Kategorien dynamisch während der Verarbeitung. Die Werte der vorherzusagenden Attribute
von Objekten sind nicht vorgegeben. Der Algorithmus muss z.B. eine Einteilung in Kategorien selbst finden anhand von Ähnlichkeits/Abstandsmassen, die auf Menge der Tupel definiert sind.
Typischerweise sind diese Verfahren dann sinnvoll, wenn auf der Menge der Tupel Ähnlichkeitsstrukturen vorhanden sind oder vermutet werden, die inhaltlich interpretiert werden können. Deshalb eignen sich Clusteringverfahren besonders, um große Mengen von Dokumenten zu strukturieren und Beziehungen zwischen den Dokumenten zu erkennen.
Das Clustering besteht aus drei Teilschritten:
Berechnung der Ähnlichkeit der Objekte untereinander:
Dieser Schritt ist sehr stark von der Art derObjekte, bzw.deren
formaler Repräsentation abhängig. In jedem Fall muss ein
Ähnlichkeitsmaß (z.B. Skalarprodukt ) oder Abstandsmaß
definiert werden.
Erstellung einer Ähnlichkeitsmatrix für alle möglichen Paare
aus der Menge von Objekten (z.B. Dokumentenpaare aus
Dokumentensammlung).
Die Aufgabe besteht darin, N Objekte in M Klassen aufzuteilen,
wobei in der Regel M nicht bekannt ist.
Die Klassenbildung soll so stattfinden, dass die Cluster die
zugrundeliegende Struktur der Objektmenge repräsentieren.
Das wird durch die Forderung erreicht, dass zwei Objekte eines
Clusters in Bezug auf das Ähnlichkeitsmaß(Abstandsmaß) näher
beieinander liegen als Objekte aus verschiedenen Clustern.
Die Gestalt der Cluster
hängt in erster Linie von drei Einflussgrössen ab:
der Aufbereitung der Daten, etwa Termgewichtung oder Einsatz von Stopwortlisten,
dem verwendeten Ähnlichkeits- oder Abstandsmaß,
dem Clusteringverfahren
Aufbereitetung der Daten
Eine wichtige Überlegung vor dem eigentlichen Clustering ist die Wahl der Features, mit denen die Dokumente charakterisiert werden. Oft benutzt man für Textdokumente die enthaltenen Wörter.
Nicht alle Wörter tragen jedoch den gleichen Informationsgehalt.
Wie auch sonst im Information Retrieval üblich sollten Funktionswörter , über Stopwortlisten aus den Texten herausgefiltert werden und nicht zum Clustering herangezogen werden, weil sie das Ergebnis des Clustering verfälschen können, da sie häufig in sehr vielen Texten vorkommen und wichtigere Clustersrukturen überdeckt werden.
Die Wahl der Stopwortliste hängt dabei auch sehr stark von der Art der betrachteten Dokumente ab.
Die Auswahl der Stopwörter stellt also in gewissem Rahmen berets eine Vorklassifikation der Dokumente anhand der erwarteten Klassen dar.
Ferner treten Worte nicht unabhängig voneinander auf, sondern sind bestimmte Wortgruppen häufiger gemeisam anzutreffen als andere. Diese Eigenschaft kann man ausnutzen, um die Anzahl der Dimensionen des zu untersuchenden Vektorraums zu verringern, indem mit mathematischen Methoden diese Abhängigkeiten ermittelt und die Term-Dokument-Matrix entsprechend umgerechnet wird. Auch kann Stemming und Lemmatisierung dieselbe Rolle beim Dokumentenclustering spielen.
Beim Dokumentenclustering wird davon ausgegangen, dass die dokumente (di) durch einen Dokumentenvektor repräsentiert sind
di = ( di1, di2, ..., din ), n = |Wortliste|
Die Terme können nach verschiedenen Kriterien bewertet werden:
Solche Kriterien sind beispielsweise die Häufigkeit des Auftretens des Stichwortes im Dokument, oder der Ort des Vorkommens im Dokument.
Die Werte der einzelnen Koordinaten eines Dokument-Vektors im Dokumentenraum entsprechen dann z.B. der Termfrequenz multipliziert mit einem Gewicht der in diesem Dokument vorkommenden Termen.
Koordinaten von Termen, die in dem Objekt nicht vorkommen, erhalten den Wert Null.
Mit der Zuordnung von Vektoren zu den Dokumenten hat man auch eine Möglichkeit geschaffen, ein Maß für die Ähnlichkeit von Dokumenten abZuleiten: je geringer die Distanz zweier Punkte (Vektoren in Dokumentenraum) isr, desto ähnlicher sind auch die Inhalte der korrespondieRenden Dokumente.
Möglichkeiten müssen gefunden werden, um die Ähnlichkeit von Dokumenten in Zahlenwerten auszudrücken, damit Clustering-Methoden auf eine Menge von Dokumenten angewendet werden können.
Funktionen die diese Aufgabe erfüllen heißen Ähnlichkeitsfunktionen.
Ähnlichkeits-und Abstandsfunktionen
Ähnlichkeitsmaße(S) beschreiben die Ähnlichkeit zwischen zwei Objekten (Dokumenten) i und j in Bezug auf die untersuchten Variablen (der Wortliste).
Sei O eine Menge von Objekten, Q die rationalen Zahlen, dann
ein Ähnlichkeitsmaß S wird definiert als:
S: O x O -> Q wenn gilt
S (i, j) = S(j, i) ;
S(i, i) > S(i, j) für alle j != i
Analog zu einem Ähnlichkeitsmaß ergibt sich eine „Unähnlichkeit“
oder ein Abstand zwischen zwei Dokumenten A(i,j) = 1-S(i,j).
ein Abstandsmaß A wird definiert als:
A: O x O -> Q und gilt
A(i, j) = A(j, i) ;
A(i, j) = 0 gdw. i = j ;
A(i, k) + A(j, k) > A(i, j)
Das zweite Schritt des Clusterings besteht in der Erstellung einer Ähnlichkeitsmatrix für allemöglichen Dokumentenpaare aus der Dokumentenmenge.
Für verschidene Werte einer Ähnlichkeitsmatrix, die aus Ähnlichkeitsmaßen aufgebaut ist, gilt:
je grösser das Ähnlichkeitsmaß zwischen zwei Dokumenten ist, desto ähnliche sind sie.
Für verschidene Werte von Abstandsmaßen gilt:
je kleiner das Abstandsmaß zwischen zwei Dokumenten ist, desto ähnlicher sind sie.
Allerdings muss man bei der Interpretation der Matrix die Spezifika des gewählten Ähnlichkeits/Abstandsmaßen berücksichtigen.
Clustering - Methoden werden üblicher Weise nach der Cluster-Struktur, die sie erzeugen, eingeteilt.
Clusteringverfahren
nicht hierarchische
teilen eine Menge von N Dokumenten auf M Cluster auf.
Hierbei sind keine Überlappungen erlaubt, d.h. jedes Objekt gehört nur einem Cluster an, dem es am ähnlichsten ist.
Ein vollständiges Clustering liegt erst nach dem letzten Schritt vor.
Jedes Cluster wird entweder durch Clusterzentrum oder durch ein Dokument des Clusters repräsentiert.
hierarchische
erzeugen verschachtelte Datenmengen, wobei jeweils Paare von Dokumenten bzw. Clustern sukzessive miteinander verbunden werden, solange bis jedes Dokument in die Hierarchie eingegliedert ist.
Hierarchische Methoden können entweder zusammensetzend oder zerteilend sein.
Bei jedem Schritt kann man das Verfahren abbrechen.
Hierarchische Clusteringverfahren
bauen aus einer gegebenen Menge von Objekten schrittweise Cluster auf. Bei jedem Schritt kann man das Verfahren aufhören.
Nach der Art des Vorgehens unterscheidet man:
a) zusammensetzende (agglomerative) Verfahren: man beginnt mit einer Menge von „Clustern“, die aus jeweils einem Dokument bestehen.
In jedem Schritt werden zwei dieser Cluster, bzw. Cluster,
die in vorhergehenden Schritten erzeugt wurden, miteinander zu
einem neuen Cluster verbunden.
Die Verfahren enden, wenn alle Elemente der Grundmenge zu
einem einzigen Cluster verschmolzen sind.
b) zerteilende (divisiven) Verfahren: man beginnt mit einem Cluster, der alle Elemente der Grundmenge enthält.
Dieser wird schrittweise in kleinere Cluster aufgespalten (bzw. diese Cluster werden geteilt), bis jeder Cluster nur noch aus einem Element besteht.
| Agglomerativ | Divisiv | |
|---|---|---|
| Startzustand: | Menge von N ein-elementigen, disjunkten Clustern | 1 Cluster mit allen N Objekten |
| Endzustand: | 1 Cluster mit allen N Objekten | Menge von N ein-elementigen, disjunkten Clustern |
| Clusteringschritt | Vereinige die beiden einander am nächsten liegenden Objekte bzw. Cluster | Teile einen bestehenden Cluster in zwei Teile |
Bei den Vorgehensweisen ( a, b ) gemeinsam ist eine festgelegte
Richtung, in der die Clusterbildung voranschreitet. Einmal getroffene
Entscheidungen ( Zusammenfügungen oder Aufteilungen) werden nicht
revidiert. Damit können auch Fehlentscheidungen nicht rückgängig
gemacht werden.
Ferner liefern hierarchische Clusteringverfahren keine eindeutige
Lösung, wann die optimale Aufteilung der Grundmenge erreicht ist,
da sie immer am Ende, nachdem letzten Schritt:
- entweder einen grossen Cluster liefern, der alle Elemente enthält
(bei agglomerativen Verfahren),
- oder eine Menge von Clustern mit nur einem Element
(bei divisiven Verfahren).
Daher muss eine andere Methode gefunden werden, um zu
entscheiden, wann die „optimale“ Anzahl von Clustern erreicht ist.
Wie bereits erwähnt liefern hierarchische Methoden nicht mehr ausschließlich eine strikte (bestimmte) Kategorisierung von Dokumenten in Clusters, sondern auch eine Clusterhierarchie.
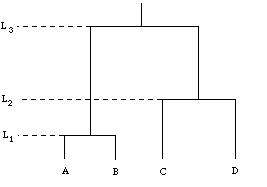
Die Clusterstruktur wird oft in Form eines "Dendrogramms" visualisiert.
Dendrogramm
D(A) + D(B) = Cl(AB);
D(C) + D(D) = Cl(CD);
Cl(AB) + Cl(CD) = Cl(ABCD)

Dadurch wird die Folge der paarweisen Verbindungen von den Objekten dargestellt, und die Höhe der Balken gibt Auskunft über die Ähnlichkeit der verbundenen Dokumente.
In dem in gezeigten Beispiel, wurden in einem ersten Schritt die Dokumente A und B als jene Dokumente identifiziert, die sich einander am ähnlichsten sind. A und B wurden deshalb zu einem Cluster zusammengefaßt, was durch die Verbindung von A und B durch einen Balken veranschaulicht wird. Ein Cluster wird in weiterer Folge wie ein einzelnes Element behandelt. Im nächsten Schritt wurde festgestellt, daß sich die Dokumente C und D nun am ähnlichsten sind. Auch sie wurden zu einem Cluster verbunden.
In der anschließenden Verarbeitungsstufe stellte sich dann heraus, daß die zwei bisher gefundenen Cluster den größten Ähnlichkeitswert besitzen. Die beiden Cluster werden deshalb in einem übergeordneten Cluster zusammengefaßt. Durch diese Vorgehensweise entsteht eine hierarchische Struktur zwischen den Clustern.
Sobald Objekte mit Clustern verbunden werden, stellt sich die Frage, wie die Abstände dieser Gruppen zu den anderen Objekten oder die Abstände zwischen zwei Clustern ermittelt werden. Wie können wir den Abstand zwischen Cl ( A,B ) und Cl ( C,D ) bestimmen und sehen, dass er der kürzeste aller Abstände ist?
Die Entfernung der Elemente wird mit verschiedenen Methoden ermittelt. Ein sehr einfache solche Methode ist das Single-Linkage-Verfahren. Hier ist der Abstand zwischen zwei Gruppen (Clustern mit einem oder mehreren Elementen) die geringste Entfernung zwischen zwei Elementen der beiden Gruppen.
Sei (ab) der Cluster aus den Dokumenten a und b , dann ist der Abstand von Cl(ab) zum Dokument k das min der Abstände zwischen a und k ; und b und k : A((ab),k)) = min[A(a,k), A(b,k)]
Nach dieser Regel ergeben sich für die folgende Beispielmatrix der Abstände:
|
|
D1 |
D2 |
D3 |
D4 |
D5 |
|---|---|---|---|---|---|
|
D1 |
0 |
|
|
|
|
|
D2 |
2 |
0 |
|
|
|
|
D3 |
6 |
5 |
0 |
|
|
|
D4 |
10 |
9 |
4 |
0 |
|
|
D5 |
9 |
8 |
5 |
3 |
0 |
Der kleinste Abstand beträgt 2 Einheiten zwischen den Dokumenten 1 und 2,
also werden diese beiden zu einem neuen Cluster verschmolzen. Wir müssen zwischen diesem neuen Element und den alten die neuen Abstände berechnen.Wir tun das über das min und man erhält die neue Abstandsmatrix:
|
|
C(D1,D2) |
D3 |
D4 |
D5 |
|---|---|---|---|---|
|
C(D1,D2) |
0 |
|
|
|
|
D3 |
5 |
0 |
|
|
|
D4 |
9 |
4 |
0 |
|
|
D5 |
8 |
5 |
3 |
0 |
Im nächsten Schritt werden die Objekte 4 und 5 ( 3 - min ) vereinigt, und man erhält ein neuen Element- Cl(45). Man muss die Abstände zwischen Elementen berechnen:
|
|
C(D1,D2) |
D3 |
C(D4,D5) |
|---|---|---|---|
|
C(D1,D2) |
0 |
|
|
|
D3 |
5 |
0 |
|
|
C(D4,D5) |
8 |
4 |
0 |
Nun haben die Elemente Cl(D4,D5) und D3 den kleinsten Abstand in der Absrandsmatrix, und man erhält Cl(D3,D4,D5):
|
|
C(D1,D2) |
C(D3,D4,D5) |
|---|---|---|
|
C(D1,D2) |
0 |
|
|
C(D3,D4,D5) |
5 |
0 |
Im letzten Schritt werden noch diese beiden Cluster vereinigt zu Cl(D1,D2,D3,D4,D5):
|
|
C(D1,D2,D3,D4,D5) |
|---|---|
|
C(D1,D2,D3,D4,D5) |
0 |
Genau entgegengesetzt zum Single Linkage Clustering arbeitet das Complete-Linkage-Verfahren. Der Abstand zwischen einem neu gebildeten Cluster und den übrigen ist nun der Abstand zwischen den beiden entferntesten Elementen der beiden Cluster:

Der Abstand von Cl(ab) zum Dokument k das max der
Abstände zwischen a und k ; und b und k :
A((ab),k)) = max[A(a,k), A(b,k)]
Wenn wir alle Abstände zwischen Elementen beim Complete-Linkage-Verfahren berechnet und Abstandsmatrix ausgefüllt haben, wählen wir immer den kleinsten Abstand zwischen zwei Elementen aus der Abstandsmatrix aus und vereinigen diese Elemente. Denn der kleinste Abstand zw. Elementen bedeutet, dass ihre Ähnlichkeit am grössten ist, und unser Ziel ist es, die ähnlichsten Elementen zu vereinigen.
Eine wichtige Bemerkung:
Beim Single-Linkage-Verfahren bekommen wir häufig lang gestreckte, ausGedehnte, weitVerzweigte Cluster, weil es zur Aufnahme
eines weiteren Elements in den Cluster genügt, dass ein Element des Clusters in der Nähe dieses Elements liegt. Aus diesem Grund bringt das Verfahren manchmal nicht das erwartete Ergebnis.
Auf diesem Bild kann man sehen, dass 2 intuitiv ofensichtliche Cluster mit einander verbunden werden bevor jedes einzelne abgeschlossen ist. Denn intuitiv würde man den rechten Cluster wahrscheinlich erst dann als abgeschlossend betrachten, wenn die Elemente ... in ihn aufGenohmmen sind.
Beim Complete-Linkage-Verfahren müssen alle Elemente des Clusters in der Nähe des Elements liegen, damit es in den Cluster aufGenohmmen werden kann. Deshalb werden hier in der Regel relativ scharf abgeGrenzte, runde Cluster ergeben. Auf diesem Bild sehen wir, dass wenn wir in diesem Fall das Complete Linkage Verfahren anwenden, diese Elemente ... eine grössere Chance haben in den Cluster aufGenohmmen zu werden.
Eine weitere Methode zu Entfernung-Berechnung zwischen zwei Gruppen ist Group-Average Clustering: Hier wird der mittell Wert aus den Entfernungen aller Punkte des einen Clusters zu denen des anderen Cluster berechnen.
Der Abstand zwischen zwei Clustern C(D1,D2) und C(D3,D4,D5) wird berechnet:
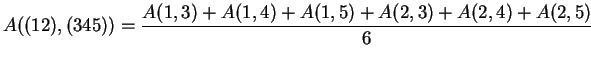
Ergibt Cluster mittlerer Grösse.
Centroid Clustering
Hier werden Cluster durch ihren Zentroid repräsentiert, einen künstlichen Vektor, dessen Komponenten aus dem Mittelwert dieser Komponente über alle Elemente des Clusters gebildet wird. Die Abstände der Cluster zuEinander sind nun die Abstände ihrer jeweiligen Zentroide.
Ein Centroid ist der Mittelpunkt eines Clusters und muss nicht unbedingt tatsächlich einem Element entsprechen.
Beispiel: angen. die Elemente sind Dokumentvektoren
(di1, di2, di3, ..., din ) für 1 <= i <= k .
Dann lässt sich ein Centroid berechnen durch
(z1, z2, z3, ..., zn), wo
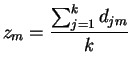
Berechnung des Abstands zwischen Cluster (D1,D2) und Cluster (D3,D4,D5) beim Centroid Clustering:
1. Bestimme den Zentroid des Clusters (12):
Dokumentvektoren D1 und D2 haben die Gestalt:
|
D1 |
D2 |
Z(12) |
|---|---|---|
|
1 |
1 |
1 |
|
2 |
4 |
3 |
|
0 |
0 |
0 |
Bestimme den Zentroid des Clusters (345):
Dokumentvektoren D3 , D4 und D5 haben die Gestalt:
|
D3 |
D4 |
D5 |
Z(345) |
|---|---|---|---|
|
1 |
1 |
1 |
1 |
|
2 |
1 |
0 |
1 |
|
2 |
2 |
2 |
2 |
Mit der Hilfe einer Abstandsfunktion bestimme den Abstand
zwischen den Vektoren Z(12) und Z(345).
Eine allgemeine Formel zur Berechnung von Abständen zwischen zwei Clustern , mit der einige von den anderen Methoden nachgebildet werden können, entwickelten Lance und Williams. Der Abstand eines neuen Clusters, der aus den beiden Clustern i und j gebildet ist, zu einem Cluster k berechnet sich als:
Ak(ij)= aiAki + ajAkj + ßAij + g| Aki - Akj |
mit Aij als Abstand zwischen den Clustern i und j .
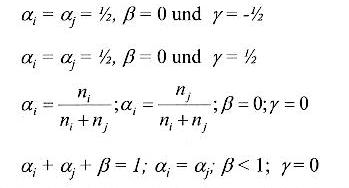 Single
Linkage
Single
Linkage
Complete Linkage
Group Average
Wenn man sich nicht für eines der drei Verfahren (Single- Complete-Linkage-Verfahren, Group-Average Clustering) entscheiden will, gibt es die Möglichkeit mit Hilfe dieser Formel und geeigneter Wahl der Parameter ai, aj , ß und g eine Kompromiss Formel zu finden.
Beispielweise wenn wir wählen:
ai=1/2, aj=1/2 , ß=0 und g=-1/2 , dann simmulieren wir Single-Linkage Formel:
A(k,(ij)) = min[A(k,i), A(k,j)]
Nicht hierarchische Methoden
Die nicht hierarchischen Methoden sind meist heuristischer Natur, da Entscheidungen über Clustergrößen, Kriterien für eine Clusterzugehörigkeit und Formen der Clusterrepräsentation gefunden werden müssen.
Die große Anzahl an Möglichkeiten die N Dokumente auf M Clusters, wobei M unbekannt ist, aufzuteilen machen eine optimale Entscheidung unmöglich.
Nicht hierarchische Methoden versuchen eine Annäherung zu erreichen, indem sie die Dokumentenmenge in geeigneter Weise partitionieren und anschließend jedes Dokument eine Partition zuweisen, zu der es am besten paßt.
Diese Variante des Clusterings hat den Vorteil, daß sie heufig effiziente schneller ist als hierarchischen Methoden.
Bei hierarchische Methoden haben wir nach jeden Schritt ein volständiges Clustering der ganzen Dokumentmenge; wir können uns enscheiden, ob wir mit dem Clustering zufrieden sind oder noch ein Schritt ausfüllen wollen.
Bei nicht hierarchischen Methoden werden zwar auch mehrere Schritte durchgeführt, aber ein volständiges Clustering liegt erst nach dem letzten Schritt vor.
Diese Methoden sind relativ einfach, da die Menge der Dokumente nur einmal bearbeitet werden muß. Der Folgende Algorithmus soll die prinzipielle Arbeitsweise dieser Methoden veranschaulichen.
Verallgemeinerte Algorithmen
"Single Pass" Methoden
Der erste Cluster wird durch das erste Dokument D1 repräsentiert.
Berechne für ein Dokument Di die Ähnlichkeiten S zu allen bereits existierenden Clustern
Wenn das Maximum Smax aus Schritt 2 größer als ein Schwellwert ST ist, dann weise das Dokument Di dem entsprechenden Cluster zu, und berechne die Repräsentation des Clusters neu. Ist Smax kleiner als ST, dann erzeuge mit Di einen neuen Cluster.
Wenn es noch Dokumente Di gibt, die noch keinem
Cluster angehören, dann setzte bei Punkt 2 fort.
Als Repräsentation eines Clusters kann beispielsweise das geometrische Zentrum aller Dokumente dieses Clusters dienen. "Single Pass" Methoden haben zwar den Vorteil, daß sie relativ simpel sind, aber sie besitzen auch die Eigenschaft, daß sie vorallem in der Anfangsphase verhältnismäßig große Cluster bilden. Außerdem sind die gebildeten Cluster abhängig von der Reihenfolge, mit der die Dokumente abgearbeitet werden.
Aus diesem Grund werden diese Methoden auch dazu verwendet, um eine erste Partitionierung der Dokumente zu erreichen, die dann als Ausgangspunkt für andere Algorithmen, wie beispielsweise "Reallocation" Algorithmen, dient.
"Reallocation" Methoden
Diese Methoden benötigen eine Partitionierung der Dokumente als Ausgangsbasis. Die Dokumente werden dann entsprechend von Cluster zu Cluster verschoben um die Partitionierung zu verbessern.
Allgemeiner "Reallcation" Algorithmus:
1. Gegeben sind M Clusters
2. For i = 1 to N, weise Di dem ähnlichsten Cluster zu
3. For j = 1 to M, berechne die Zentren der Cluster neu
Wiederhole die Schritte 2 und 3 solange, bis sich in
der Zuordnung der Dokumente zu den Clustern
kaum mehr etwas ändert.
N ist die Anzahl der Dokumente und M die Anzahl der Cluster.
Wir haben jetzt gesehen, daß die unterschliedlichen Clustering-Verfahren zu sehr verschiedenen Ergebnissen führen: Beispielsweise erhält man bei Anwendung der Single-Linkage-Methode langgestreckte, verzweigte Cluster, während z.B. beim Group Average Linking eher runde Cluster entstehen.
Die Gestalt und Verteilung der Cluster ist also abhängig vom gewählten Gesamtverfahren, Abstands- bzw. Ähnlichkeitsmaß und der Methode, nach der Abstände zwischen Clustern bestimmt werden.
Ebenso beeinflußt die Präparation der Dokumente (Auswahl der relevanten Terme, Zuordnung von Gewichtsfaktoren usw.) das Ergebnis.
Kriterien für die optimale Kombination aller einflußnehmenden Faktoren lassen sich nur schwer angeben (fixieren); natürlich ist zwar beispielsweise ein Verfahren, das sphärische Cluster liefert, für eine Dokumentenmenge mit (natürlich gegebener) sphärischer Strukturierung sehr gut geeignet - aber die natürlich gegebene Strukturierung ist normerweise nicht erkennbar.
Für ein gegebenes Clustering-Problem müssen also unter Umständen mehrere Verfahren ausprobiert und die Ergebnisse verglichen werden, d.h. dasjenige Ergebnis muß ausgewählt werden, das dem menschlichen Betrachter intuitiv am besten gefällt.



Cluster-Retrieval
Das Cl-R stellt ein Retrieval Verfahren dar, d.h. es geht darum, aus der Dokumentenmenge solche Dokumente automatisch auszuwählen, die für ein gegebennes Query relevant sind. Dabei benutzt man im Prinzip das Vektorraum-Modell, bestimmt aber nicht die Ähnlichkeit jedes einzelnen Dokuments zum Query, sondern berechnet mit Hilfe eines ClusteringVerfarens Cluster und bestimmt dann nur die Ähnlichkeit der Cluster-Zentroide zum Query. Als Suchergebnis werden dann nur die Dokumente zurückgegeben, die in einem Cluster liegen, dessen Zentroid als relevant.
Hier im Bild sind die Dokumente der Dokumentenmenge als Quadrate dargestellt : Nicht alle Dokumente werden hinsichtlich ihrer Relevanz bewertet, sondern nur die Zentroide der zugehörigen Cluster (= Kreise) werden mit dem Query-Vektor verglichen. Die relevanten sind hier grau schraffiert (und zwar ist ein Zentroid "relevant", wenn er einen ausreichend kleinen Abstand zum Query-Vektor hat).
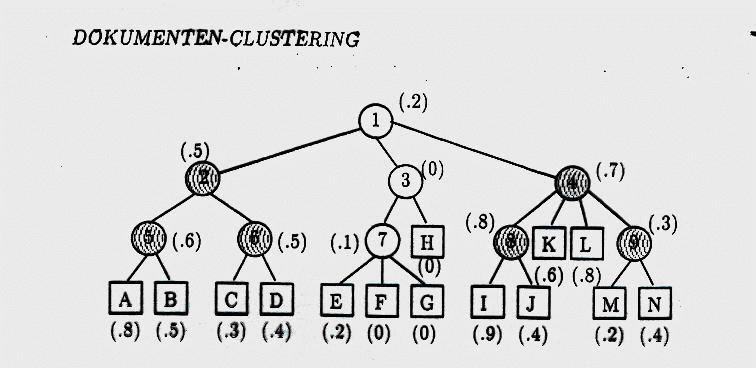
In diesem Fall ist ein hierarchisches Clustering-Verfahren angewandt worden, deshalb gibt es Zentroide auf mehreren Ebenenen: Nummer 1 ist der Zentroid für den alles-umfassenden Cluster (wie er am Ende eines agglomerativen Verfahrens herauskommt). Nummer 2, 3 und 4 sind die drei Cluster, die zwei Schritte vor dem Ende des Clustering bestanden haben usw. D.h. es wurden die Ergebnisse jedes Zwischenschritts des hierarchischen Verfahrens benutzt (das
Clustering-Verfahren wurde also nicht nach dem n-ten Schritt gestoppt und die dann vorhandenen Cluster verwendet): Die ganze Hierarchie wird benutzt.
Für das Suchergebnis bewerten wir anschließend nur die Dokumente (mit dem üblichen Vektorraum-Modell, d.h. der Abstand jedes Dokumentvektors zum Query-Vektor), die einem schraffierten (= relevanten) Cluster liegen. D.h. die Dokumente E, F, G und H kommen für das eigentliche Retrieval-Verfahren gar nicht mehr in Frage.
Der Effekt des Cluster-Retrieval besteht also nur darin, die Menge der für das eigentliche Retrieval betrachteten Dokumente zu verringern, d.h. sozusagen die Suchmenge einzuschränken.
Der Vorteil liegt dann darin, daß weniger Dokumente bzw. Dokumentvektoren untersucht werden müssen. Außerdem werden bei dieser Art von Retrieval nicht nur die Zusammenhänge zwischen Dokumenten und Query, sondern auch die Zusammenhänge unter den Dokumenten berücksichtigt (weil man ja die Ergebnisse des Clustering benutzt, und für das Clustering spielen nur Beziehungen der Dokumente untereinander eine Rolle, nicht Beziehungen zum Query (denn beim
Clustering ist das Query ja noch gar nicht bekannt)).
In Experimenten zeigte sich aber leider , daß die
Retrieval-Ergebnisse beim reinen Vektorraum-Retrieval besser sind.
Eine weitere Anwendung von Cluster-Verfahren ist das Term-Clustering. Hier werden nicht Dokumente, sondern Wörter (Terme) geclustert, also gruppiert - z.B. hinsichtlich ihrer Zusammengehörigkeit: Als Ähnlichkeitsmaß verwendet man dann beispielsweise die Kookkurrenz: je häufiger zwei Wörter gemeinsam (d.h. in einem Text oder Paragraphen) vorkommen, desto ähnlicher sind sie.
Als Cluster ergeben sich dann Gruppen von irgendwie thematisch zusammengehörenden oder sogar synonymen Wörtern. D.h. das Ergebnis des Term-Clustering ist eine Art Thesaurus. Clustering-Verfahren dienen hier als Unterstützung bei der automatischen Erstellung von Thesauri.